Topological Sort

Dangers and Annoyances: Make sure you have a way of reading in directed graphs. In a directed graph, when you encounter an edge from a to b, you should not automatically create an edge from b to a.

Graph data.

• Example 1, 7 vertices.
• Example 2, 23 vertices.
• Example 3, 43 vertices.
• Example 4, 94 vertices.
• Example 5, 192 vertices.

There is also code to generate a random directed acyclic graph linked below in the Timing section.

Verification code

Write code to verify that a list of vertices is in topologically sorted order.

Just check that the given vertices are ordered so that a vertex that appears later in the list does not connect to a vertex earlier in the list. No need to check for pathologies like missing vertices or other random errors.

• Example 6, with 11 vertices, along with a topologically sorted list of vertices and a list that is not topologically sorted.

def is_topological_sort(g: Graph, topo: List[Vertex]) -> bool:
    return false

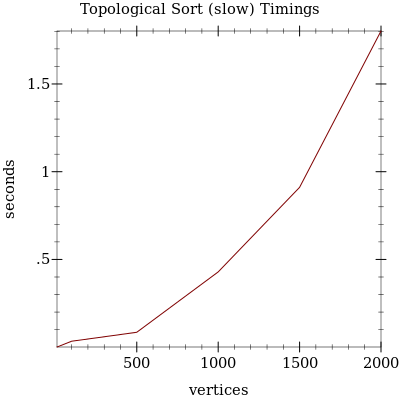
Timing

We want to compare the slow method (also called “naive”) and a faster method of finding a topologically sorted order for the vertices of a graph.

Produce a graph of speed of execution vs number of vertices, for n in [10,100,500,1000,1500,2000]. When you are totally done, you will have two lines:

• Slow method (do as soon as you have a working slow method)
• Faster method

Use a random 20% chance of creating each edge in the code to make a random directed acyclic graph.

Timing information should not include the construction of the random graph. Typical timing code would look like this:

import timeit
# ...
def do_timing():
    g = ... build random graph ...
    work_f = lambda : topological_sort(g)
    t = timeit.timeit(work_f, number=10)
    return(t/10)

Random Questions

• Why do you need to work with directed acyclic graphs for topological sort? What if the graph were not directed? What if the graph were not acyclic?
• In a topologically sorted ordering, does switching the positions of unconnected siblings (vertices that share the same parent and do not have an edge between them) still give you a topologically sorted ordering of the verties? Explain.

• ←Previous
Next→